
 2)x2+(a-1)x+3=0
2)x2+(a-1)x+3=0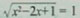
首頁 > 初三 > 數(shù)學(xué) > 上學(xué)期 > 正文

 2)x2+(a-1)x+3=0
2)x2+(a-1)x+3=0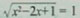

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》3.4 直線與圓的位置關(guān)系(第四課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》3.4 直線與圓的位置關(guān)系(第三課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》3.4 直線與圓的位置關(guān)系(第二課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第4章《一元二次方程》綜合練習(xí)(第三課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第4章《一元二次方程》綜合練習(xí)(第二課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第4章《一元二次方程》4.7 一元二次方程的應(yīng)用(復(fù)習(xí)與鞏固)

九年級(jí)數(shù)學(xué)上冊(cè)第4章《一元二次方程》4.4 用因式分解法解一元二次方程

九年級(jí)數(shù)學(xué)上冊(cè)第4章《一元二次方程》4.3 用公式法解一元二次方程(復(fù)習(xí)與鞏固)

九年級(jí)數(shù)學(xué)上冊(cè)第4章《一元二次方程》4.3 用公式法解一元二次方程(第二課時(shí))
 正在播放
正在播放
九年級(jí)數(shù)學(xué)上冊(cè)第4章《一元二次方程》4.1 一元二次方程(第一課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第4章《一元二次方程》4.3 用公式法解一元二次方程(第一課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》綜合練習(xí)(第四課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》綜合練習(xí)(第三課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》綜合練習(xí)(第二課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》綜合練習(xí)(第一課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》3.7 正多邊形與圓(復(fù)習(xí)與鞏固)

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》3.7 正多邊形與圓(第二課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》3.7 正多邊形與圓(第一課時(shí))

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》3.6 弧長(zhǎng)及扇形面積的計(jì)算(復(fù)習(xí)與鞏固)

九年級(jí)數(shù)學(xué)上冊(cè)第3章《對(duì)圓的進(jìn)一步認(rèn)識(shí)》3.6 弧長(zhǎng)及扇形面積的計(jì)算
評(píng)論0
點(diǎn)此登錄 后即可暢所欲言